2 The 4 Technology Solutions

 
HEAT IN GROUNDWATER SYSTEMS PART I - THE FUNDAMENTALS

An On-Line Version of a Column First Published in the:
National Environmental Journal Vol. 6 No. 2 Mar./Apr. 1996 Page 30-31

by: David B. Vance  dbv7@mindspring.com

Of the many parameters that are monitored in association with the assessment and remediation of contaminated groundwater, temperature is typically regarded as a background condition that must be accepted for a given site. In the northern tier of states it is customary that in the winter months remediation processes will be slowed or stopped depending upon the depth of groundwater. This and the next column will be focused on the issue of heat in groundwater systems. This column will cover the overall thermal behavior of groundwater systems.

First some definitions are required:

• Heat is added or external energy that causes a rise in temperature, expansion, evaporation or other physical change.
• The rise or drop of temperature in an aquifer is the result of the transport of heat into or away from the aquifer.
• The key measure of the relationship between heat flow and resulting temperature is heat capacity, C_p.
• For the purpose of this column heat capacity will be used as specific heat in English units, which is the number of BTUs required to raise one pound of aquifer matrix by one degree Fahrenheit.

 There are two primary materials that through which heat is transported in an aquifer, the mineral matrix and the entrained groundwater. Density of the mineral matrix and water, porosity, and heat capacity combine to govern the temperature response of an aquifer to heat flow. The specific heat C_p (as BTU/lb⁰F), dry density (rho, as lbs/ft3) and percent porosity (phi) of some soils and minerals are as follows:
 

 The thermal energy capacity per unit volume per degree of temperature change is termed the aquifer thermal capacity (q). With the above information it is possible to calculate the thermal capacity (q) of an aquifer:

q = (C_p x rho)_rock(1 - phi) + (C_p x rho)_water x phi

Assuming a sandy aquifer with a specific heat of 0.19 for the mineral matrix, a density of 110 lbs/ft³, and a porosity of 0.35 the specific thermal capacity per cubic foot of aquifer is:

• q = (0.19 x 110)_rock x (1 - 0.35) + (1.0 x 62.4)_water x 0.35
• q = 13.59_rock + 21.84_water = 35.4 BTU per cubic foot per 1 degree Fahrenheit

 Now as an example, given a volume in an aquifer 100 feet by 100 feet by 20 feet in depth, it would require 7,080,000 Btu to raise the temperature 1 degree Fahrenheit. Converting BTU to Kilowatt hours gives 2,073 Kilowatt hours. At 6 cents per KW, that is equal to $ 125 in electrical cost. That estimate does not take into account the efficiency of the heat generation system, transfer of that heat into the aquifer, and effects of heat transport away from the zone undergoing heating.

There are three physical processes responsible for heat transfer in groundwater systems:

• Conduction - heat flows from hotter regions to cooler regions through the molecular transfer of kinetic energy.
• Convection - heat is transported along with overall mass transport of groundwater.
• Radiation - the transference of heat through space via electromagnetic radiation.

 The dominant mechanisms in groundwater systems are convection and conduction.

Thermal conductivity (k) is the amount of heat that will flow through a unit area in a unit time with a unit temperature difference. Under saturated conditions the value of thermal conductivity is primarily governed by the texture, degree of compaction and mineralogical composition of the aquifer matrix. Thermal conductivity decreases with the reduction of particle size. The units of thermal conductivity are Btu per hour per foot per degree Fahrenheit. Typical values are as follow:

• Water 0.346
• Air 0.0145
• Wet Sand 0.95
• Dry Sand 0.157
• Wet Clay 0.87
• Dry Clay 0.138

 Notice that the thermal conductivity of water is about 23 times that of air. In the past, the use of heat as an augmentation to remediation has been applied to the vadose zone through the application of steam. In terms of heat transport efficiency, that is probably not the most efficient application of a subsurface heating process.

Heat flow through a mass (qx) is calculated by the equation:

qx = Ak(dT/dX)

• A is the cross sectional area normal to the heat flow,
• k is the thermal conductivity,
• T is temperature in Fahrenheit,
• X is the distance over which the heat must flow.

 The solution to the above function requires substitution of an equation describing the system geometry for the dX term followed by integration. That is beyond the scope of this column.

Thermal diffusivity (in units of square feet per hour) is equal to the thermal conductivity (k) divided by the thermal capacity (q) of the aquifer, it measures the rate at which temperature changes occur in the soil mass. Higher values of thermal diffusivity result in more rapid changes in temperature and deeper penetration of heat into the soil.

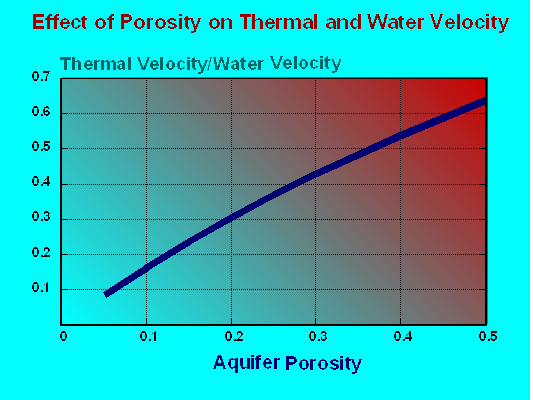
Ratio of Thermal Velocity to Groundwater Velocity Versus Porosity

Lastly, as heated groundwater moves through an aquifer thermal energy is transferred to the mineral matrix. As a consequence the thermal front associated with the advective flow of heated groundwater will move at a lower velocity than the groundwater. Aquifer porosity is the dominant element in this dynamic. The Figure was prepared ignoring site specific small scale details of heat transport dynamics and treating an aquifer in bulk. The graph shows the ratio of the velocity of the migration of the thermal front versus the groundwater velocity as effected by aquifer porosity. The smaller the ratio, the slower the thermal front velocity compared to overall groundwater velocity.

Next column, the effect of heat on the remediation process.

Return to the Environmental Technology Index Page

Copyright 2008 David B. Vance
All Rights Reserved

If you have comments or suggestions, e-mail me at dbv7@mindspring.com